1.1 The system equations
Analog simulator starts an analysis by writing a set
of nodal equations which describe the components of the circuit. According
to KCL -Kirchoff Current Low the nodal equations for a circuit may be built
by summing the currents leaving each of the circuit nodes. Let us take
as example the following circuit:
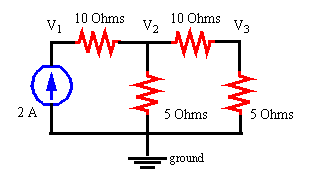
-2 A + (V1 - V2)/10 Ohms = 0 - notation for V1 node
(V2 - V1)/10 Ohms + V2/5 Ohms + (V2 - V3)/10 Ohms = 0 -
notation for V2 node
(V3 - V2)/10 Ohms + V3/5 Ohms = 0 - notation for V3 node
After a simple algebraic transformation we obtain:
1.0* V1 - 1.0*V2
= 20
-1.0* V1 + 4.0*V2 + 1.0*V3 = 0
-1.0* V2 + 3.0*V3 = 15
These three equations have three unknown voltages (V1,V2,
V3). We will rewrite them in the form of a matrix and we will apply Gaussian
elimination to solve them.
1.0*V1 - 1.0*V2 + 0.0*V3 = 20
-1.0*V1 + 4.0*V2 + 1.0*V3 = 0
0.0*V1 - 1.0*V2 + 3.0*V3 = 15
Matrix form:
1.0 - 1.0 + 0.0
V1 20
-1.0 + 4.0 + 1.0 * V2
= 0
0.0 - 1.0 + 3.0
V3 15
Applying forward elimination we obtain:
1.0 - 1.0 + 0.0 V1 20
0.0 + 3.0 + 1.0 * V2 = 20
0.0 + 0.0 + 10.0 V3 65
The value of V3 is 6.5 volts; the voltages V2 and V1
may be determined by applying back-substitution resulting in:
V2 = (20 - 6.5) / 3.0 = 13.5/3.0 = 4.5 volts
V1 = (20 + 4.5) /1.0 =24.5 volts
