 Introduction to VHDL-AMS
Introduction to VHDL-AMS
The VHDL (Very High Speed Integrated Circuit Hardware
Description Language) is a powerful language for the description of digital
circuits. With the VHDL, it is possible to simulate and synthesize the
digital circuits for different technologies. The already created entities
are archievable in libraries and may be adapted for reuse. This in turn
favors the productivity while the predefined components may be integrated
into more complex systems.
The first standardization of VHDL has taken place in
1987. In 1993, an improved version has been standardized. It had to allow
to integrate the analog system modeling but still a lot of work was necessary
to achieve this aim. A specific group has been organized to develop an
extension to the language that could allow the description and the simulation
of digital-analog hybrid systems. This expanded release has for name VHDL-AMS
(AMS: Analog and Mixed Signal) and has been standardized recently as IEEE
- VHDL 1076.1. standard (
http://www.vhdl.org/vi/analog).
The aim of this presentationis is to introduce the final
release of VHDL-AMS, the new mechanisms provided to model analog phenomena
and to interconnect digital and analog models. To illustrate these mechanisms
we will provide some simple analog components described in VHDL-AMS. The
presented descriptions are analyzed using VHDL-AMS analyzer available at
http://www.ecs.soton.ac.uk
More details on the VHDL-AMS including the tutorials in english and french
may be found in VHDL CODE LAND environment (
http://www.ireste.fr/fdl)
Purpose of
this standard
The purpose of VHDL-AMS standard was to provide a hierarchical description
and continuous and mixed system simulation. The language had to support
the modeling of different levels of abstraction in electrical and some
non-electrical domains (e.g. systems built from of hydraulic or mechanical
components). The analog circuits can be modeled by systems of differential
and algebraic equations(DAE). The resolution of these systems had to include
the management of discontinuities. On the other hand it was necessary to
respect the constraints relative to different levels of the interactions
between numerical section and analog part of hybrid systems.
One sees therefore that the analog behavior specificity
and hybrid systems modeling induced the creation of a certain number of
new mechanisms such as:
-
the creation of an analog resolution nucleus to solve systems of equations,
and a notation for these systems of equations,
-
the creation of new quantities to express differences of potential at terminals
of a path and the crossing it current as well as the notion of tolerance,
-
a redefinition of the cycle of simulation for the simulation of hybrid
systems and creation of concurrent commands.
Continuous system description
The continuous aspects of behavior of analog system
aimed by VHDL-AMS can be described by an algebraic and differential system
of equations (DAE) with the time as independent variable.
These equations are the form:
F(x,dx/dt,t)
where x is the vector of unknowns, dx/dt vector of derivatives
of the unknowns with respect to time, and t is time.
Most of these systems of equations have no analytical solution,
therefore practically some solutions have to be approximated by using digital
techniques. The unknowns of a DAE are analytic functions of the time. They
are continuous by intervals with a finite number of discontinuities. The
algorithms of digital resolution solve a DAE system simultaneously for
the values of all the unknowns in all instances determined by the algorithm.
No object of VHDL obtains these values of a such manner.
For this reason a new class of object is created for the unknown of DAE:
the quantity.
Quantities are built from one or several sub-items of
float type in order to approximate continuous values . An object quantity
can appear in an expression or, everywhere where a value of this type is
authorized. Continuous features of a composed quantity are simply the set
of features of each of these scalar sub-items. Each sub-item behavior is
independent to others. Quantities can be declared everywhere where a signal
can be declared excepted in a package.
The following declaration creates a quantity of real
type:
quantity ra :real;
The quantity object can also be used for ports defined
in an entity. Such a quantity is called a port quantity , by analogy
to a port signal. Port quantities have a mode (in,out), the in same
manner as port signals.
entity simple is
port (quantity
qin2: in real);quantity
qout:out real);
end simple;
When this entity is instantiated each quantity of port
is constrained to have the same value that the quantity with which it can
be associated through instantiation.
The language defines a number of implied quantities necessary
for writing of DAEs.
For each quantity Q:
-
Q'Dot indicates the quantity of the same type that Q that represents the
derivative of Q in respect to time.
-
Q'Integ indicates a quantity of the same type that Q that represents the
integral of Q over time, from time 0.0 to current instant.
For derivatives of superior orders, it suffices to write:
Q'Dot'Dot (order 2) and for integrals Q'Integ'Integ (integral order 2).
Tolerance group
The tolerance under VHDL-AMS is based on the notion of
tolerance group. A tolerance group is the collection of solution elements
- quantities and characteristic expressions of the model - that have the
same degree of tolerance. Typically, elements of solutions in a tolerance
group have the same order of precision.
Tolerance group of a quantity in a solution is specified
by the model. The binding of tolerance group to a quantity can be postponed
until the moment of instantiation.
Note that tolerance groups are not specified by definition
because they depend on the algorithm used for the DAE resolution and its
software.
subtype voltage is
real tolerance "maxtol_vol";
subtype current is
real tolerance "maxtol_cur";
quantity qvol: voltage;
quantity qcur: current;
The derivatives or integrals of qvol inherit the tolerance
of qvol.
Conservative
systems
Conservative electrical systems are obeying to laws of
Kirchhoff. The description of conservative systems uses the theory of graphs.
In VHDL-AMS , one uses branch quantities that are decomposed in two members,
the across quantities that represent voltages and through quantities that
represent the currents. Note that accross/through quantities may also represent
other physical phenomena such as velocity/force or temperature/heat_float.
For example, a resistance is a path governed by the law
of Ohm that connects the tension levels of its terminals (across quantity)
and specifies the current that crosses it (through quantity). Note that
resistance is a two-terminal path to be declared with two terminals. Resistance
terminals are types of simple nature. Simple nature depends on the domain
(electrical, thermal, hydraulic...).
In the following example we declare two subtypes: voltage
and current with their respective tolerances and a simple nature electrical.
Then we declare two terminals of this nature, and a quantity v across the
terminals and a current i through the same terminals t1 to t2.
subtype voltage is
real tolerance - " tol_voltage" ;
subtype current is
real tolerance - " tol_current" ;
nature electrical is
voltage across current through;
terminal t1, t2: electrical;
quantity v across
i through t1 to
t2;
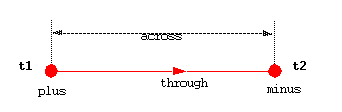
v is the difference of potential between terminals, that
is the typical voltage and has for code of tolerance "tol_voltage" and
i represents current through the path and its tolerance is "tol_current".
The two terminals are called plus and minus, the way
of the path is plus to minus, that is the positive flow of the current.
In the following example, one declares an array of nature
type and a subnature of this vector type:
nature electrical_vector
is array(natural range
<>) of electrical;
subnature el_vect4 is
electrical_vector(0 to 3);
terminal t3, t4: el_vect4;
quantity vpp across
ipp through t3 to
t4;
quantity vps across
ips through t1 to
t4;
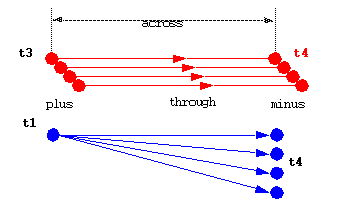
The tolerance group of a path is determined by its subtype.
It is possible to redefine it in the subnature of the declaration or in
the declaration of the path. The next example declares a subnature low_voltage
with the appropriate tolerance than are declared two terminals of this
subnature and two quantities between these terminals.
subnature low_voltage
is electrical;
tolerance "tol_lowvoltage"
across "tol_lowcurrent" through;
terminal tx, ty: low_voltage;
quantity vlow1 across
ilow1 through tx to
ty:
Tolerances of vlow1 and ilow1 are defined by the declaration
subnature, it is "tol_lowvoltage" for voltage and "tol_lowcurrent" for
current.
The predefined attributes 'across and 'through allows
to extract the nature corresponding to the object. Given the above declarations,
tx'across is voltage and tx'through is current.
Terminal, like a signal can be a port of an entity. The
following example shows a simple model with two terminals, the input terminal
terin and the output terminal terout:
entity simple is
port (terminal
terin, terout:electrical);
end simple;
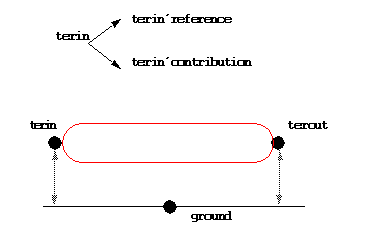
The reference terminal of the terminal terin of nature
nat is designated by terin'reference.
If a path is declared with only one terminal, than the
other one (default terminal) is ground terminal. The ground is considered
as minus terminal.
The declaration of terin creates two quantities:
-
the reference quantity terin'reference, that is an across quantity between
the two terminals plus and minus.
-
the contribution quantity, terin'contribution that is a through quantity
equal to the sum of all quantities incident to terin.
Simultaneous statements (assignments).
The description of continuous behavior needs a new kind
of notation not available in VHDL 1076. This notation is introduced to
VHDL-AMS as simultaneous statements. Simultaneous statement allows to express
the systems of differential algebraic equations (DAEs). It is built from
ordinary VHDL expressions, but the interpretation on the resultant value
and the behavior differ from the evaluations relative to VHDL 1076 assignments.
The analog solver determines the value of each quantity
such that the values of all characteristic expressions are close to zero
and thus solves the DAEs of the model. Simultaneous statement assignment
can take place everywhere where a signal assignment is allowed. The basic
syntax of simultaneous statement is as follows:
[label:] simple_expression == simple_expression;
The expression may refer to quantities, signals, constants,
shared variables, literals and functions. For example a constitutive equation
of a resistor may be written as:
i == v/r;
where v is an across quantity representing voltage between
the two terminals and r the value of the resistance. The following are
two examples, one of a simple resistor and one of a simple capacitor model:
entity resistor is
generic(r:real:=1.0E3);
port (terminal
rin, rout:electrical);
end resistor;
architecture simple
of resistor is
begin
quantity v across
i through rin to
rout;
begin
i == v/r; -- characteristic expression
end simple;
entity capacitor is
generic(r:real:=1.0E-9);
port (terminal
capin, capout:electrical);
end capacitor;
architecture simple
of capacitor is
begin
quantity v across
i through capin to
capout;
begin
i == c*v'dot; -- characteristic
expression
end simple;
Each expression and each characteristic quantity belongs
to a tolerance group. By default, the tolerance group for a characteristic
expressions with a simple simultaneous statement whose left part is the
name of a quantity, is the tolerance group of this quantity. Otherwise,
the designer of the model has to specify the tolerance group during the
declaration.
For example, the tolerance group may defined during the
declaration as follow:
i == c*v'dot tolerance
"tol_lowcurrent";
Simulation time and
cycle
The synchronization between the analog solver and the
event driven simulation kernel of VHDL requires a common formalism for
time representation in the continuous and discrete simulation domains.
This requirement was satisfied by the introduction of the Universal_Time
type, by analogy with Universal_Integer and Universal_Real.
Universal_Time has a precision of float type which is
sufficient to image the time exactly. There are two time variables of Universal_Time
type maintained by the simulator: the kernel variable Tc, that represents
the running time of the simulation, and Tn, that indicates the following
time. The function now is defined to return the value of the running simulation
time (Tc ). This value is of Universal_Time type, resolved after truncation
to a nearest value of the current time. There is another function now that
returns the value current simulation time aligned to the nearest value
of the real time.
The predefined attribute S'Last_Event,
returns an effective time value corresponding to the elapsed time since
the last event on S.
The simulation cycle has been adapted to take into account
the time used by the analog solver. The analog solver is activated in each
simulation cycle, just before the current time (Tc) is advanced. The sequence
of solutions to the DAEs (Analog Solution Points -ASP) are located in suitable
intervals between the the current time (Tc) and the next event instance.
In this manner, the value of a quantity received by a digital process as
well as the value of digital signal appearing in simultaneous assignments
are always correct.
Interaction A/D and
D/A
If one of the quantities crosses a specific value considered
as threshold before the end of the calculation of the solution (next event),
the analog solver will end the solution cycle prematurely. A boolean attribute
above was introduced to detect the thresholds. For the scalar value Q,
a boolean signal with value true is generated by Q'above(level) if Q>level,
and false otherwise. The detection of the overflow of a threshold can be
used for the Analog - Digital (AD) conversion:
entity sadc is
-- simple analog to digital converter
generic (niveau: real:=
2.5); -- threshold
port (terminal
at: in electrical; -- analog input
signal ds: out bit);
-- digital output
end sadc;
architecture simple
of sadc is
quantity vq across
at; - - across quantity to ground
begin
ds <= `1' when vq'above(level)
-- vq > level
else `0'; -- vq <level
end simple;
A digital process that is sensitive to a such quantity
generates an event at the exact time which may have no representation in
physical type time. Such a time is called offset time. Any process resuming
as a consequence of a delta-delayed signal assignment in a process executing
at an offset time also executes at the same offset time.
However any delayed signal assignment occurs at a time
exactly representable in physical type time, converted by truncation.
If a discontinuity appears in the solution of the DAE
a specific break mechanisms ( break) indicates it to analog solver. Break
generates a pseudo-event each time when a discontinuity is detected. A
discontinuity may appear in a simultaneous statement using a signal when
an event intervenes on this signal.
The execution of a break statement generates an implicit
signal used to reactivate the analog process. The semantics of the language
requires that the solver assumes the discontinuity when the process containing
to the signal break is active. The declaration of break provides also a
means to specify the initial conditions for selected quantities to be applied
after discontinuity.
The following examples illustrates the use of break statement
in a simple DA converter:
entity sdac is
generic (vdd: real:
= 3.3); -- vdd constant for analog output
port (signal ds: in
bit; -- logic input
terminal at: out
electrical); -- analog output
end sdac;
architecture simple
of sdac is
quantity v across
at; - - branch quantity to ground
begin
if s ='0' use
v==0.0; -- low output
else
v==vdd; -- high output
end use;
break on s; - - prevision
of discontinuity
end simple;
A model has to include an appropriate break declaration
if the name of a signal appears in an expression of a simultaneous statement
and if an event on this signal may cause discontinuity. Break instruction
is also required if a discontinuity is due to the selection of a new simultaneous
statement when the value of an if condition changes (see the example above).
User
specified initialization and quiescent point
The solution of a system DAE in a continuous interval
depends solely on the unknowns at the beginning of interval. These values
have to be solutions of the DAE. They depend on initialization process
and possibly on a number of other equations derived from the original ones.
The continuous model has to be initialized with a suitable algorithm before
the simulation begins and does have to be reinitialized at each discontinuity.
In general, there are several initial conditions that
satisfy the DAE, because during the initialization there are more unknowns
that equations ( x and dx/dt are the unknowns during the initialization).
The selection of a particular set of values depends on additional parameters
and on the convention chosen by user.
An analog model built with VHDL-AMS distinguishes between
the effective initialization, that expands the initialization scheme defined
for VHDL and the operational initialization looking for a quiescent point.
The quiescent point represents the DC operating point of the model.
The language defined the quiescent point of a model as
the state of the solution immediately before the postponed processes are
about to be executed at time 0.0.
In the absence of user specified initialization conditions,
the quiescent point is specified by:
dx/dt = 0
Note that the initial conditions are specified by the user
employ the same break instruction that is used to specify the discontinuities:
break
qval1 => expression1, qval2 => expression2;
The simulator kernel controls the driver of the predefined
signal DOMAIN of enumerated type DOMAIN_TYPE. During the initialization,
the value of the signal DOMAIN is indexed to INITIALIZATION_DOM. When the
quiescent point has been found the kernel assigns a new value to the signal
DOMAIN: TIME_DOMAIN if the quiescent point has been found during a temporal
simulation, and FREQUENCY_DOMAIN if the simulation is frequential. Consequently
the postponed process is skipped to an other delta cycle to update the
signal DOMAIN. This means that it is possible reinitialize a process when
the quiescent point has been found, and to define the way used o find the
quiescent point, in temporal or in frequential simulation.
Modeling
and simulation in the frequential domain
VHDL-AMS includes resolutions that support simulations
in the noise and in alternative regime in a Spice-compatible manner, based
on a small signal model derived from equations (1). The small signal model
is defined by the linear term of the series expansion of Taylor with the
respect of all quantities, the system (1) obtained for the value of the
signal DOMAIN: FREQUENCY_DOMAIN, with the partial derived trial to the
stable point of job. The small model signal is an incremental linear model
described by a system of linear equations with incrementation of quantities
of the unknowns. Consequently, the results of the small signal model simulation
are only approximations of the true physical behavior of the system. The
system of equations describing the small signal model is homogenous unless
the model specifies some specific stimuli in the frequential domain. The
defined language provides two specific source quantities: the spectral
source that defines the stimuli for frequential simulation and the noise
source that specifies the noise characteristics. Both sources quantities
have to be declared with the help of a special syntax and their type can
be a composite type. A simple example below shows a model of a source of
current. Its value is composed from a constant current (dcurr) and a spectral
source q_ac combined with noise source q_ns :
entity complex_current_source
is
generic (dcurr, ac_amplit,
ac_phase, noise_amplit: real:=0.0);
port (terminal tplus,
tminus: electrical);
end complex_current_source;
architecture example
of current_source is
quantity i through
tplus to tminus;
quantity quant_ac: real
spectrum ac_amplit, ac_phase;
quantity quant_noise:
real noise ns_amplit;
begin
i == dcurr + quant_ac + quant_noise;
end example;
Expressions defining the amplitude for a source quantity
or the phase for a spectral source are VHDL expressions. They can include
names others quantities, that allow, for example, to define sources of
bias dependent noise. Moreover, these expressions can include calls to
the function FREQUENCY that returns the frequency of current simulation.
It is the only place where this function can be called; it is to tell that
the language supports the stimuli in the frequential domain but does not
support the frequential simulation behavior.
Using multiple disciplines
The conservative systems described with VHDL-AMS may
be modeled with different physical natures including thermal, mechanical
and many other disciplines. The generalized effort quantities are specified
as voltage, temperature or force; the generalized flow quantities are specified
as current, heat flow or velocity.
The following example is a model of a diode with self
heating implies two disciplines: the electrical discipline and the thermal
discipline.
package my_disciplines
is
subtype volt is
real tolerance "voltage";
subtype temp is
real tolerance "temperature";
subtype curr is
real tolerance "current";
subtype heatflow is
real tolerance "heatflow";
nature electrical is
volt across curr through;
nature thermal is
temp across heatflow through;
alias el_ground is
electrical'reference;
alias th_ground is
thermal'reference;
end package my_disciplines;
A simplified model of a self heating diode may be expressed
using the following equations:
Id= Is *(e(Vd-Rd*Id)/Vt -1)
Vt= Td * Boltzmanc/Charge_el = Td/11
600
Pd= Vd * Id
where:
Vd - diode voltage, Is - saturation current, Rd - diode
resistance, Vt - thermal voltage, Pd - dissipated power, e - 100.43 Boltzmanc
= 1.3806226e-23, Charge_el = 1.602191e-19
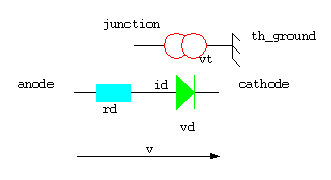
use work.my_disciplines.all
use IEEE.math_real.all;
entity my_diode is
generic(is0: real:=
1.0e-13; rd: real:= 1.0);
port(terminal
anode,cathode: electrical; terminal junction:
thermal);
end my_diode;
architecture simple
of my_diode is
quantity vd across
id through anode to
cathode;
quantity vt: voltage;
quantity temp across
power through ground_th to
junction;
constant volt_equivalent:
voltage:11,600.0;
begin
id == is0*(exp((vd -rd*id)/vt) - 1);
vt == temp/volt_equivalent;
power == v * id; -- thermal power
end simple;
Procedural style of
descriptions
VHDL-AMS allows a user to describe DAEs using a sequential
style. The simultaneous procedural statements can include any sequential
statements of the VHDL language, except signal assignments and wait statements.
The following example is a model of a mos transistor
described using procedural style:
package mos_param is
type mosmodel is
record
nss: real;
tox: real;
eg: real;
phim: real;
i: real;
mun: real;
na: real;
vbs: real;
end record mosmodel;
type mos_type is
(nmos, pmos);
constant epsilon_s0:
real := 8.85418e-12;
constant epsilon_ox:
real := 3.9*epsilon_S0;
constant epsilon_si:
real := 11.7*epsilon_S0;
constant electron_charge:
real := 1.602191e-19;
constant boltzmann:
real:= 1.380226e-23;
constant ni: real:=
1.45e16;
end package mos_param;
use mos_param.all;
use IEEE.math_rael.all;
entity mos is
generic(most:mos_type:=
nmos;width,length:real:= 100.0e-6;
model:mos_model:=(nss:
real:= 1.0e11; tox: real:= 1.0e-9; phims: real:= 0.8;
mun: real:=;
na: real:=1.45e17; vbs: real:= 0.0));
port(terminal:
drain, gate, source, bulk: electrical);
end mos;
architecture levelone
of mos is
quantity id through
drain;
quantity vbs across
bulk to source;
quantity vds across
drain to source;
quantity vgs across
gate to source;
begin
mos_proc:
procedural
variable lambda,vt,phif,phims,cox,qss,vfb,gamma,vt0,beta:
real;
begin
if most=nmos then
lambda:= 1.0;
else lambda= -1.0;
vt= boltzmann*temp/electron_charge;
phif =vt* ln(na/ni);
cox := epsilon_ox/tox;
qss := nss*electron_charge;
vfb := phims - qss/cox;
gamma := sqrt(2*electron_charge*epsilon_si*na)/cox;
vt0 := vfb + 2*phif + gamma*sqrt(2*phif - vbs) -
sqrt(2*phif));
beta := mun*cox*width/length;
if vds < (vgs - vt0)
use
id := beta*(1+lambda*vds)*((vgs-vt)*vds - vds**2/2);
else
id := (beta/2) *(1+lambda*vds)*(vgs-vt)**2;
end use;
end procedural;
end levelone;
The following example is a model
of a cmos inverter described using the definition of mos transistor
above:
use mos_param.all;
use IEEE.math_rael.all;
entity inverter is
port(terminal
cmosin, cmosout: electrical)
end inverter;
architecture cmos of
inverter is
component mos
generic(mos_type: most;width,length:real;
model:mos_model:=(nss:
real ; tox: real; eg: real; phim: real;
ki: real
; mun: real ; na: real ; vbs: real: ));
port(terminal:
drain, gate, source, bulk: electrical);
end mos;
constant vdd: voltage:=
3.3;
begin
inmos: generic
map(most:mos_type:= nmos;width,length:real:= 100.0e-6;
model:mos_model:=(nss: real:= 1.0e11; tox: real:= 1.0e-9; phims: real:=
0.8;
mun: real:=; na: real:=1.45e17; vbs: real:= 0.0));
port(terminal:
cmosout, cmosin, ground, ground: electrical);
ipmos: generic
map(most:mos_type:= pmos;width,length:real:= 100.0e-6;
model:mos_model:=(nss: real:= 1.0e11; tox: real:= 1.0e-9; phims: real:=
0.8;
mun: real:=; na: real:=1.45e17; vbs: real:= 0.0));
port(terminal:
cmosout, cmosin, vdd, vdd: electrical);
end cmos;
Building mixed (AD)
descriptions
Below we are going to describe a PLL circuit. This example
illustrates a mixed analog-digital system that exploits most of the VHDL
mechanisms provided for mixed signal modeling.
-
usage of predefined components and libraries
-
usage of behavioral and structural styles
-
a mix of analog and digital components
The basic architecture of a PLL is shown in figure below.
It consists of a phase detector, a low-pass filter, a gain stage, and a
voltage controlled oscillator (VCO) configured in a loop. The phase detector
is a circuit that normally has an output voltage with an average value
proportional to the phase difference between the input signal and the output
of VCO. The low pass filter is used to extract the average value from the
output of the phase detector. This average value is then amplified and
used to drive the VCO. The negative feedback of the loop results in the
output of the VCO being synchronized with the input signal. The low pass-filter
is an RC low_pass filter of first order. The phase detector described below
is a combination of digital circuits such as D flip-flops. When CMOS technology
is used, the VCOs may be implemented as ring oscillator with fully differential
inverters. In our description the VCO is described at behavioral level.
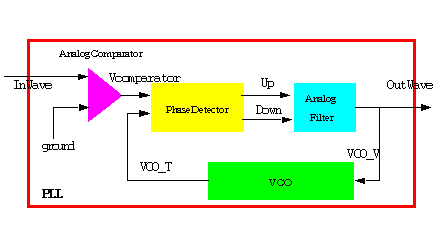
The description of the complete system is preceded by
the definition of components.
 VCO : behavioral
description
VCO : behavioral
description
Entity declaration:
entity VCO is
generic(
fc: real := 1E6; -- cut-off frequency fc for the
tension Vc
df: real := 0.5E6; -- [Hz/V], rapport frequency/tension
Vc: voltage := 0.0 -- tension for central frequency
);
port( quantity
Vin: in voltage; terminal
OutTerminal: electrical);
end VCO;
Architecture definition of VCO :
architecture PhaseIntegrator
of VCO is
constant TwoPi: real
:= 6.283118530718; -- 2pi
quantity Phase : real;
-- phase is a free quantity:
quantity Vout across
Iout through OutTerminal to
ground;
begin
break Phase => 0.0;
-- break allows to define the initial conditions
break Phase => Phase
mod TwoPi on Phase'above(TwoPi);
-- break allows to keep the phase interval between
0 and 2pi.
Phase'dot == TwoPi*realmax(0.5E6,
fc+(Vin-Vc)*df); -- phase statement
Vout == 2.5*(1.0+sin(Phase)); -- output statement
end PhaseIntegrator;
 Analog
comparator: behavioral description
Analog
comparator: behavioral description
Entity declaration.
entity AnalogComparator
is
generic( Vthreshold:
voltage := 0.0 ); -- [V] threshold tension
port(terminal
Pve_T,Nve_T: electrical; -- analog entry
signal Out_T: out BIT
); -- digital output
end AnalogComparator;
Architecture definition of analog comparator:
architecture Behavior
of AnalogComparator is
quantity DeltaV across
Pve_T to Nve_Y; -- tension at differential
entry
begin
-- the architecture consists of one concurrent signal
assignment statement
Vout <= `1' when
DeltaV'above(0.0)
-- trigger event when V+>V-
else `0' when
not DeltaV'above(0.0);
-- trigger event when V+<=Vt-
end Behavior;
 Phase detector
: structural description
Phase detector
: structural description
Entity RS flip-flop declaration:
entity RSFF is
generic (DelayQ, DelayQB:
TIME := 0 ps);
port ( SB,RB: in bit;
Q,QB: out bit);
end RSFF;
The definition of RS flip-flop architecture:
architecture Behavior
of RSFF is
begin
-- set Q as a NAND operation
Q <= SB nand QB after
DelayQ;
-- set QB as a symmetrical NAND operation
QB <= RB nand Q after
DelayQB;
end Behavior; -- RSFF
Structural description of phase detector with RS flip-flop:
entity PhaseDetector
is
port( In1,In2 : in
bit; Up,Down: out bit);
end PhaseDetector;
architecture Structural
of PhaseDetector is
signal UpB,DownB,TQ,SUp,RDown,BQB,M
: bit; -- internal signals
component RSFF is
-- components used in the architecture
port( SB,RB: in
bit; Q,QB: out bit);
end component;
begin
SUp <= M and TQ;
RDown <= M and BQB;
M <= not( TQ and
UpB and DownB and
BQB);
-- instantiation of RS flip-flops
RST: RSFF port map(
SB=>UpB, RB=>M, Q=>TQ, QB=>open );
RSB: RSFF port map(
SB=>M, RB=>DownB, Q=>open, QB=>BQB );
RSUp: RSFF port map(
SB=>SUp, RB=>M, Q=>Up, QB=>UpB );
RSDown: RSFF port map(
SB=>M,RB=>RDown,Q=>DownB,QB=>Down );
end Structural; -- PhaseDetector
 Analog filter
definition:
Analog filter
definition:
entity AnalogFilter
is
generic (InCurrent :
current := 100E-6; -- [A] input current
-- generic values for components
R1: REAL := 100E3; R2: REAL := 10E3;
C1: REAL := 100E-12; C2: REAL := 3.3E-9 );
port (signal
Up,Down : bit;
-- the signals controlling charge-pump phase comparator
terminal Filter_T: electrical
-- analog output pin );
end AnalogFilter;
architecture Circuit
of AnalogFilter is
terminal Vc1_T,Vc2_T
:electrical; -- internal node
quantity Isource through
Vc1_T to ground; -- courrent source
begin
-- equations modeling the behavior of current sources
if Up = `1' and
Down = `0' use Isource == 100E-6; -- 100mA
elsif Up = `0' and
Down = `1' use Isource == -100E-6; -- -100ma
else Isource == 0.0;
-- no current;
-- instantiation of filter components
C1: capacitor generic map (100E-12)
port map(Vc1_T,ground);
R1: resistor generic map (100E3)
port map(Vc1_T,Vfilter);
R2: resistor generic map
(10E3) port map(Filter_T,Vc2_T);
C2: capacitor generic map
(3.3E-9) port map(Vc2_T,ground);
end Circuit;
Description of PLL: assembling
the basic components.
entity PLL is
port(terminal
InWave_T,OutWave_T: electrical);
end PLL;
architecture MixedSignal
of PLL is
signal Vcomparator,Up,Down,Vcounter,VCO_D
: bit; -- internal signals
terminal Filter_T,VCO_T
: electrical; -- internal terminals
quantity Filter_V across
FilterT to ground; -- tension at filter output
quantity VCO_V across
VCO_T to ground; -- tension at VCO output
component AnalogComparator
is
port(terminal
Pve_T,Nve_T: electrical; -- analog inputs
signal Vout : out bit ); -- digital
output
end component;
component PhaseDetector
is
port( In1,In2
: in bit; Up,Down : out
bit );
end component;
component AnalogFilter
is
port (signal
Up,Down: bit; -- digital inputs
terminal Filter_T: electrical ); -- analog output
end component;
component VCO is
port(quantity
Vin: in voltage;terminal
Out_T : electrical);
end component;
begin
Comparator_L: AnalogComparator port
map (Pve_T => InWave_T, Nve_T => ground,
Vout => Vcomparator );
PhaseDetector_L: PhaseDetector port
map ( In1 => Vcomparator, In2 => VCO_T, Up => Up, Down => Down);
Filter_L: AnalogFilter port
map (Up => Up, Down => Down, Filter_T => VCO_V );
VCO_L: VCO port map
( Vin => VCO_V, Out_T => VCO_T );
-- analog to digital conversion of VCO output
VCO_D <= `0' when
VCO_V'above(2.5) -- logic threshold 2.5V
else `1' when not VCO_V'above(2.5);
end MixedSignal; --
PLL
The above introduction to VHDL-AMS should allow the potential
users to understand its basic mechanisms and possible application areas.
VHDL-AMS is a new standard but is coming as an extension of mature VHDL
environments. This will allow for its rapid expansion in the domain of
mixed-signal designs. The driving force will be the need to model and implement
mixed analog-digital systems on chip. New compiler/simulation tools for
VHDL-AMS are going to be available from many companies Analog, FTL Systems,
Mentor Graphics, (
http://www.analog.com,
http://www.ftlsystems.com,
http://www.mentorg.com)
Meanwhile the SPICE to VHDL-AMS translators and analyzers
pave the way for a widespread reception of VHDL-AMS.
 Introduction to VHDL-AMS
Introduction to VHDL-AMS Introduction to VHDL-AMS
Introduction to VHDL-AMS




![]() Analog filter
definition:
Analog filter
definition: