|
[실전 강의실 VHDL]
|

|
하드웨어 설계, 이제는 프로그래밍으로! 3
나의 첫 하드웨어 프로그래밍, 자판기 프로젝트
지난 두 번의 연재를 통해 다양한 디지털 회로의 구현 방법과 대표적인 하드웨어 기술 언어인 VHDL에 대해 살펴봤다. '백문이 불여일행'이라 했던가. 이제는 직접 실습을 해 볼 차례이다. 먼저 기초적인 디지털 회로에 대한 프로그래밍을 수행할 것이다. 이를 바탕으로 좀더 복잡한 자판기의 동작을 묘사할 수 있는 하드웨어 모듈을 설계해 보자.
|
연재순서
|
|
|
|
|
1회 2002.8 | 최상의 하드웨어 설계 방법을 찾아라
|
|
2회 2002.9 | 완벽한 하드웨어 기술언어, VHDL
|
|
3회 2002.10| 나의 첫 하드웨어 프로그래밍, 자판기 설계 프로젝트
|
|
|
|
연재가이드
|
|
|
|
|
운영체제 | 윈도우 98 이상
|
|
개발도구 | Xilinx Foundation (PC & UNIX)
|
|
기본지식 | 논리 회로, 디지털 시스템
|
|
응용분야 | 디지털 회로의 설계, ASIC/FPGA의 설계
|
|
|
|
|
|
곽종욱 celot@naver.com
|
|
|
|
하드웨어를 디자인할 수 있는 언어 VHDL과 Verilog 프로그래밍에 관심을 갖고 있으며, 링 기반 고성능 대형 컴퓨터 개발 프로젝트에 참여한 바 있다. 자신을 하드웨어 엔지니어라고 소개하는 필자는 이 글을 통해 디지털 시스템 설계와 하드웨어 기술 언어를 이용한 프로그래밍에 관심을 갖는 독자가 많아지기를 바란다고.
|
지난 연재에서 우리는 다양한 하드웨어의 설계 방법을 알아봤다. 그리고 설계하는 시스템의 특징에 따라서 여러가지 설계 방법이 존재한다는 사실을 알았다. 그 중에서도 하드웨어의 동작을 묘사할 수 있는 프로그래밍 언어인 VHDL에 대해 별도의 연재를 할애해 가면서 자세히 살펴봤다. 이번 호에서는 지금까지의 지식을 바탕으로 직접 하나하나 프로그래밍 해 보자. 본 연재에서 최종 목표로 삼은 실습 과제는 자판기의 동작을 묘사할 수 있는 하드웨어 모듈의 설계이다. 하지만 처음부터 이와 같은 모듈을 설계하기에는 기본적인 배경 지식이 필요하다. 따라서 이번 연재에서는 디지털 회로에 대한 기본 배경에 대해 설명한 뒤 이를 응용하고 주제를 좀더 확장시켜 우리의 최종 결과물인 자판기 프로젝트를 수행해 보자.
디지털 회로의 모델링
디지털 회로는 일반적으로 조합 회로(combinational circuit)와 순차 회로(sequential circiut)로 구분된다. 조합 회로는 현재의 입력이 주어지면 즉시 그에 대한 출력의 값이 결정되는 회로를 의미한다. 반면 순차 회로는 현재의 입력된 정보와 과거에 저장되어 있었던 기억 값에 의해서 출력 값이 결정되는 회로를 말한다. 즉 현재의 입력과 회로의 기억된 상태에 따라서 그 출력이 결정됨을 의미한다. 당연히 회로의 복잡도로 따지자면 순차 회로가 조금 더 복잡한 형태를 보인다. 하지만 기억할 수 있다는 특성 때문에 순차 회로가 없는 디지털 시스템은 거의 없다고 봐도 무방할 것이다. 그럼 지금부터 조합 회로와 순차 회로에 대해서 하나씩 알아보기로 하자.
조합 회로의 모델링
먼저 살펴볼 회로는 조합 회로이다. 조합 논리 회로는 앞서 설명한 바와 같이 출력이 현재의 입력에 의해서만 결정되는 회로를 의미한다. 이러한 조합 논리 회로의 기본적인 형태가 <그림 1>에 나타나 있다.
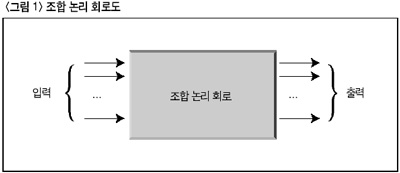
이러한 조합 논리 회로의 대표적인 예로서 기본적인 산술 연산을 가능케 하는 가산기/감산기, 그리고 외부의 입력을 내부 형태로 바꾸어 주고 또 그 반대의 동작을 취하는 인코더/디코더, 여러 입력 중에서 하나의 값을 출력하는 멀티플렉서(multiplexer), 그리고 이와는 반대의 동작을 하는 디멀티플렉서(demultiplexer), 여러 입력 값들을 비교하는 비교기(comparator) 등을 그 예로 들 수 있다. 무엇보다도 가장 대표적인 예는 바로 ALU(Arithmetic & Logic Unit)일 것이다. 흔히 컴퓨터의 메인 두뇌라 할 수 있는 CPU는 내부적으로 계산 모듈, 제어 모듈, 기억 모듈과 같은 여러 모듈로 구성되어 있다. 그 중에서 산술/논리 연산을 담당하는 모듈이 바로 ALU이다.
ALU를 모델링하자
그럼 지금부터 VHDL을 사용해 ALU를 직접 모델링해 보자. 중앙처리 장치는 기본적으로 레지스터와 같은 기억 장치, 제어 장치등 여러 세부 모듈로 이뤄져 있는데 그 중에서 제일 핵심이 되는 모듈이 바로 ALU이다. 이런 ALU야말로 순수한 조합 회로들로 이뤄져 있는 모듈이다. 더하기/빼기와 같은 산술 연산뿐만 아니라 각종 논리 연산이 가능하며 또한 n개의 입력이 있을 경우 이를 해석해 어떤 연산 모듈에 보낼 것인지를 결정한다. 앞서 예로든 조합 논리회로의 총 집합체라고 해도 과언이 아닐 것이다.
조금 더 구체화하자. 우리가 모델링할 ALU는 실제 시스템에서 사용되는 ALU보다 어느 정도 제약이 있기는 하다. 하지만 이를 확장시키고 나름대로의 최적화 과정을 거친 것이 상용화되어 있는 ALU라고 했을 때 우리가 디자인하게 될 ALU가 현실과 크게 동떨어진 것만은 아니다.
<표 1>에 우리가 구현하고자 하는 ALU의 동작을 정리했다. 이 회로는 S4부터 S0까지의 신호와 Cin의 제어 신호의 입력에 따라서 각각 두 입력, 즉 A와 B의 값을 이용해 출력 Y를 만들어 내는 역할을 하게 된다. 이들 제어 신호의 조합에 따라서 각각 산술 연산과 논리 연산 그리고 이동 연산을 수행하게 된다.
<표 1> ALU 기능도
|
S4
|
S3
|
S2
|
S1
|
S0
|
Cin
|
수행 연산
|
기능
|
구현부
|
|
0
|
0
|
0
|
0
|
0
|
0
|
Y <= A
|
A의 값 전송
|
산술 연산부
|
|
0
|
0
|
0
|
0
|
0
|
1
|
Y <= A + 1
|
A의 값 1 증가
|
산술 연산부
|
|
0
|
0
|
0
|
0
|
1
|
0
|
Y <= A + B
|
더하기
|
산술 연산부
|
|
0
|
0
|
0
|
0
|
1
|
1
|
Y <= A + B + 1
|
받아 올림이 있는 더하기
|
산술 연산부
|
|
0
|
0
|
0
|
1
|
0
|
0
|
Y <= A + B’
|
A와 B의 1의 보수와의 더하기
|
산술 연산부
|
|
0
|
0
|
0
|
1
|
0
|
1
|
Y <= A + B’+ 1
|
빼기
|
산술 연산부
|
|
0
|
0
|
0
|
1
|
1
|
0
|
Y <= A - 1
|
A의 값 1 감소
|
산술 연산부
|
|
0
|
0
|
0
|
1
|
1
|
1
|
Y <= A
|
A의 값 전송
|
산술 연산부
|
|
0
|
0
|
1
|
0
|
0
|
0
|
Y <= A AND B
|
AND
|
논리 연산부
|
|
0
|
0
|
1
|
0
|
1
|
0
|
Y <= A OR B
|
OR
|
논리 연산부
|
|
0
|
0
|
1
|
1
|
0
|
0
|
Y <= A XOR B
|
EXCLUSIVE OR
|
논리 연산부
|
|
0
|
0
|
1
|
1
|
1
|
0
|
Y <= A’
|
COMPLEMENT
|
논리 연산부
|
|
0
|
0
|
0
|
0
|
0
|
0
|
Y <= A
|
A의 전송
|
이동 연산부
|
|
0
|
1
|
0
|
0
|
0
|
0
|
Y <= shl A
|
A의 좌측 이동
|
이동 연산부
|
|
1
|
0
|
0
|
0
|
0
|
0
|
Y <= shr A
|
A의 우측 이동
|
이동 연산부
|
|
1
|
1
|
0
|
0
|
0
|
0
|
Y <= 0
|
0의 전송
|
이동 연산부
|
<리스트 1>이 <표 1>의 ALU 기능을 VHDL을 이용해 프로그래밍한 코드이다. ALU라는 하나의 엔터티를 선언했으며 이 모듈은 Sell, CarryIn 그리고 A, B를 입력으로 갖고 Y를 출력 값으로 내보내게 된다. 이와 같은 코드를 회로도로 나타내면 <그림 2>와 같이 될 것이다.
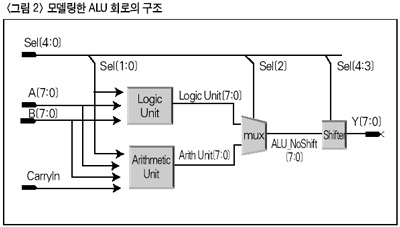
|
<리스트 1> ALU 기능 코드
|
|
-- 라이브러리의 지정 및 패키지 호출
library IEEE;
use IEEE.STD_LOGIC_1164.all;
-- 산술 연산을 위한 패키지 호출
use IEEE.NUMERIC_STD.all;
-- 엔터티의 선언문
entity ALU is
port ( -- 입력 포트
sel: in unsigned(4 downto 0);
carryin: in std_logic;
A, B: in unsigned(7 downto 0);
-- 출력 포트
Y: out unsigned(7 downto 0)
);
end entity ALU;
-- 아키텍처의 선언문
architecture ALU_body of ALU is
begin
ALU_AND_SHIFT: process(sel, A, B, carryin)
variable sel0_1_carryin : unsigned(2 downto 0);
variable LogicUnit, ArithUnit,
ALU_Noshift: unsigned(7 downto 0);
begin
-- 논리 연산 부분
Logic_Unit: case sel(1 downto 0) is
when "00"=> LogicUnit := A and B;
when "01"=> LogicUnit := A or B;
when "10"=> LogicUnit := A xor B;
when "11"=> LogicUnit := not A;
when others => LogicUnit := (others => 'X');
end case Logic_Unit;
-- 산술 연산 부분
sel0_1_carryin := sel(1 downto 0) & carryin;
Arith_Unit: case sel0_1_carryin is
when "000"=> ArithUnit := A;
when "001"=> ArithUnit := A + 1;
when "010"=> ArithUnit := A + B;
when "011"=> ArithUnit := A + B + 1;
when "100"=> ArithUnit := A + not B;
when "101"=> ArithUnit := A - B;
when "110"=> ArithUnit := A - 1;
when "111"=> ArithUnit := A;
when others => ArithUnit := (others => 'X');
end case Arith_Unit;
-- 논리 연산과 산술 연산의 멀티플렉싱
LA_MUX: if (sel(2) = '1') then
ALU_Noshift := LogicUnit;
else
ALU_Noshift :=ArithUnit;
end if LA_MUX;
-- 시프트 연산 부분
Shift: case sel(4 downto 3) is
when "00"=> Y <= ALU_Noshift;
when "01"=> Y <= Shift_left(ALU_Noshift, 1);
when "10"=> Y <= Shift_right(ALU_Noshift, 1);
when "11"=> Y <= (others => '0');
when others => Y <= (others => 'X');
end case Shift;
end process ALU_AND_SHIFT;
end architecture ALU_body;
|
순차 회로의 모델링
다음으로 알아봐야 할 회로는 순차 회로이다. 순차 회로는 무엇보다도 이전의 값이나 상태를 기억할 수 있다는 사실이 조합 회로와 비교했을 때 가장 큰 차이점이라 할 수 있다. 플립플롭(flip-flop)과 조합 논리회로들로 구성되며, 출력은 외부 입력과 플립플롭의 현재 상태에 의해 결정되는 논리 회로이다. 여기서 플립플롭이 바로 기억 장치로서의 역할을 하게 되는 것이다. <그림 3>에 이러한 순차 회로의 기본 구조가 나타나 있다.
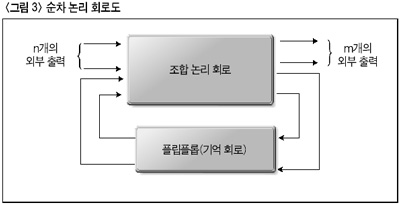
순차 회로의 대표적인 예로서 레지스터를 꼽을 수 있다. 레지스터는 CPU 내부에서 특정 데이터를 저장하고 있는 일종의 기억장치이다. 또한 카운터도 순차 회로로 구현된다. 이전의 값을 기억해야 다음 숫자나 상태를 나타낼 수 있지 않겠는가.
카운터를 모델링하자
앞서 조합 논리 회로에 대해 알아보면서 ALU를 VHDL로 직접 모델링했다. 이제는 순차 회로의 한 가지 예를 가지고 이를 모델링할 차례이다. 여기서는 카운터를 갖고 실제 VHDL로 모델링해 보기로 한다. 먼저 카운터에 대해 좀더 자세히 알아보자.
디지털 회로에서는 특정 시간 내에 입력된 클럭 수를 헤아려서(counting) 주파수를 측정하기도 하고, 동작의 순서를 제어하기도 한다. 이와 같은 용도로 카운터를 사용하며 이러한 카운터는 주로 플립플롭을 사용해 구현한다. 일반적으로 카운터는 <표 2>와 같이 외부에서 클럭이 입력될 경우 그 값이 1씩 증가하게 된다. 여기서 Q3-Q0까지의 의미는 4비트 16진 카운터를 의미하며, Q(t)는 현재 클럭이 들어오기 전의 값을 의미하고 Q(t+1)의 값은 현재의 클럭이 들어오고 난 이후의 값을 의미한다.
<표 2> 16진 카운터의 기능도
|
이전 상태
|
다음 상태
|
|
Q3(t)
|
Q2(t)
|
Q1(t)
|
Q0(t)
|
Q3(t+1)
|
Q2(t+1)
|
Q1(t+1)
|
Q0(t+1)
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
카운터는 그 동작 기법에 따라서 클럭에 동기화되어 있는 동기식(synchronous) 카운터와 동기화되어 있지 않은 비동기식(asynchronous) 카운터로 구분할 수 있다. 또한 카운터 리셋 기능의 유무에 따라서 리셋 기능이 있는 카운터와 그렇지 않고 계속 특정 값의 범위를 순환하는 순환 카운터로 구분되기도 한다. <표 3>에 방금 설명한 카운터가 예로 나타나 있다. 우리가 설계할 카운터이다. 그러면 <표 3>을 기본으로 해 실제로 모델링해 보자.
<표 3> 동기식/비동기식 리셋 카운터
|
동기식 리셋 카운터
|
비동기식 리셋 카운터
|
|
입력
|
|
출력
|
입력
|
|
출력
|
|
Clock
|
Reset
|
Q3~Q0
|
Clock
|
Reset
|
Q3~Q0
|
|
Rising Edge
|
1
|
0
|
X
|
1
|
0
|
|
Rising Edge
|
0
|
Counting
|
Rising Edge
|
0
|
Counting
|
<리스트 2>는 <표 3>에 나타나 있는 카운터 중에서 동기식 리셋 기능이 있는 4비트 16진 카운터를 나타낸다. 즉 리셋이 들어와도 클럭의 입력이 들어와야 실제로 카운터의 값이 초기화됨을 의미한다. VHDL 코드 내의 주석을 참조하면 이해될 것이다. <리스트 3>은 <표 3>에 나타나 있는 카운터 중에서 비동기식 리셋 기능이 있는 4비트 16진 카운터를 나타낸다. 즉 클럭의 입력과는 무관하게 리셋이 들어오면 바로 카운터의 값을 초기화하는 것이다.
|
<리스트 2> 동기식 리셋 카운터
|
|
-- 라이브러리의 지정 및 패키지 호출
library IEEE;
use IEEE.std_logic_1164.all;
-- 부호 없는 산술 연산을 위한 패키지 호출
use IEEE.std_logic_unsigned.all;
-- 엔터티 선언문
entity counter_4bit_sync_reset is
port (
-- 입력 포트
clock: in STD_LOGIC;
reset: in STD_LOGIC;
-- 출력 포트
q : out STD_LOGIC_VECTOR(3 downto 0)
);
end counter_4bit_sync_reset;
-- 아키텍처의 선언문
architecture counter_4bit_sync_reset_arch of counter_4bit_sync_reset is
signal counting : std_logic_vector(3 downto 0);
begin
-- <<enter your statements here>>
count : process(clock)
begin
-- 클럭의 상승 에지에서의 동작(active high)
if(rising_edge(clock))
then if(reset = '1')
-- 리셋이 1이면 출력은 0
then counting <= "0000";
-- 카운트 + 1
else counting <= counting +"0001";
end if;
end if;
end process count;
-- 카운트 값의 출력
q <= counting;
end counter_4bit_sync_reset_arch;
|
|
<리스트 3> 비동기식 리셋 카운터
|
|
-- 라이브러리의 지정 및 패키지 호출
library IEEE;
use IEEE.std_logic_1164.all;
-- 부호 없는 산술 연산을 위한 패키지 호출
use IEEE.std_logic_unsigned.all;
-- 엔터티 선언문
entity counter_4bit_async_reset is
port (
-- 입력 포트
clock: in STD_LOGIC;
reset: in STD_LOGIC;
-- 출력 포트
q : buffer std_logic_vector(3 downto 0)
);
end counter_4bit_async_reset;
-- 아키텍처 선언문
architecture counter_4bit_async_reset_arch of counter_4bit_async_reset is
begin
-- <<enter your statements here>>
count: process(clock , reset)
begin
-- 리셋이 1이면 출력은 0
if(reset='1')
then q <= "0000";
-- 클럭의 상승 에지에서의 동작(active high)
elsif (rising_edge(clock))
-- 카운터 값의 출력
then q <= q + "0001";
end if;
end process;
end counter_4bit_async_reset_arch;
|
잠깐 여기서 우리가 거쳐 온 길을 살펴보자. 우리는 지금까지 조합 회로와 순차 회로에 대해서 살펴봤다. 그렇다면 이런 것들이 자판기를 설계하는 것과 무슨 관계가 있는가라고 반문할 수 있다. 그리고 다음에서 알아볼 스테이트 머신(FSM, Finite State Machine)은 또 무엇인가. 사실 이 모든 것들이 자판기를 설계하기 위해 미리 알고 있어야 할 내용들이다. 마치 어떤 프로그래밍 언어의 문법을 안다고 해서 바로 프로그래밍이 가능하지 않는 것과 같은 이치일 것이다. 때로는 자료구조에 대한 지식도 필요하고 운영체제에 대한 지식도 필요한 것처럼 하드웨어 프로그래밍도 이와 마찬가지이다. 우리가 설계할 자판기 모듈도 조합 회로와 순차 회로가 혼합되어 있는 형태이다. 또한 이제 설명할 스테이트 머신 역시 자판기를 설계하는 데 이용하게 된다. 그럼 지금부터 스테이트 머신을 이용한 VHDL 모델링에 대해 알아보자.
스테이트 머신을 이용한 설계
스테이트 머신은 앞서 설명한 순차 회로를 제어하는 조금 더 복잡한 형태의 회로를 설계하는 데 사용된다. 순차 회로는 출력이 현재의 입력만으로 결정되는 것이 아니라 과거의 출력과 현재의 입력 및 기억된 값에 따라 출력이 결정되는데 이런 기본 구조를 바탕으로 상태(state)라는 개념을 추가한 것을 스테이트 머신이라 한다.
<그림 4>에서 보는 바와 같이 스테이트 머신은 크게 세 부분으로 나뉜다. 현재의 상태를 기억하고 있는 모듈과 다음 상태를 계산해 내기 위한 모듈 그리고 적절한 출력을 만들어 내기 위한 모듈이 그것이다. 여기서 현재의 상태를 기억하는 모듈은 순차 회로로 구성이 되며 다음 상태와 출력을 생성해 내는 모듈은 조합 회로로 구성이 된다. 그럼 이제 한 가지 예제를 통해 이러한 스테이트 머신을 이용한 VHDL 모델링에 대해 알아 보자. 이번에 구현할 예제는 레지스터이다. 레지스터는 앞서 설명한 것처럼 CPU 내부에 위치하면서 명령과 데이터를 일시적으로 저장하는 임시기억 장치로서의 역할을 수행한다. 이러한 레지스터 역시 ALU와 더불어 CPU를 구성하는 중요한 구성요소이다.
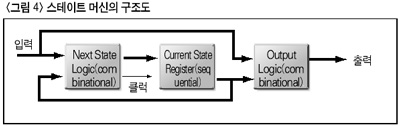
레지스터를 모델링하자
그러면 <표 4>와 같은 기능이 있는 레지스터를 구현해 보자. 실제 상용화된 CPU에서는 주로 32비트 레지스터를 사용하지만 우리가 지금 설계할 레지스터는 4비트 레지스터이다. 그리고 기능도 구현상의 편의를 위해 값의 로드 상태만을 저장하고 있는 형태로 국한시켰다. 하지만 기본적인 동작 원리는 상용화되어 있는 일반 32비트 레지스터와 유사하다. <리스트 4>에 우리가 설계할 4비트 로드 기능이 있는 레지스터의 코드가 나타나 있다.
<표 4> 4비트 레지스터의 기능
|
Input
|
|
|
|
Output
|
|
|
Clock
|
Reset
|
Load
|
Data_In3~Data_In0
|
Data_Out3~Data_Out0
|
|
|
X
|
0
|
X
|
X
|
0
|
클리어
|
|
Rising Edge
|
1
|
1
|
Data_In3~Data_In0
|
Data_In3~Data_In0
|
로드
|
|
Don't Care
|
1
|
X
|
X
|
Data_Out3~Data_Out0
|
기억상태
|
|
<리스트 4> 레지스터
|
|
-- 라이브러리의 지정 및 패키지 호출
library IEEE;
use IEEE.std_logic_1164.all;
-- 엔터티 선언문
entity register_4bit is
port (
-- 클럭과 제어 신호의 입력
clock: in STD_LOGIC;
reset: in STD_LOGIC;
load: in STD_LOGIC;
-- 데이터 입력
Data_In: in STD_LOGIC_VECTOR(3 DOWNTO 0);
-- 데이터 출력
Data_Out: out STD_LOGIC_VECTOR(3 DOWNTO 0)
);
end register_4bit;
-- 아키텍처의 선언문
architecture register_arch of register_4bit is
-- 현재 상태와 다음 상태의 선언
signal next_state, current_state : std_logic_vector(3 downto 0);
begin
-- <<enter your statements here>>
-- 현재의 상태를 출력
Data_Out <= current_state;
-- 조합 회로 부분
comb : process(current_state, load, Data_In)
begin
next_state <= current_state;
if(load='1')
then next_state <= Data_In;
end if;
end process;
-- 순차 회로 부분
seq : process(clock, reset)
begin
-- 리셋이 0이면 현재 상태 클리어
if(reset='0')
then current_state <= (others => '0');
-- 다음 상태의 결정
elsif (clock’event and clock='1')
then current_state <= next_state;
end if;
end process;
end register_arch;
|
스테이트 머신의 종류
스테이트 머신은 <그림 4>와 같이 구성되는 것이 일반적인 형태이다. 하지만 이러한 스테이트 머신 역시 구현하는 방법에 따라서 다음과 같이 두 가지로 세분화된다.
밀리 머신
우선 알아볼 스테이트 머신은 밀리 머신(mealy machine)이다. 이는 <그림 5>에서 나타난 바와 같이 출력 함수가 다음 상태와 현재의 입력에 의해서 결정되는 구조를 말한다. 따라서 입력 신호의 조건에 따라서 여러 개의 출력 신호를 가질 수 있으며 비교적 자유도가 높은 상태도를 구현할 수 있다. 하지만 외부 입력이 출력 함수에 직접 전달되기 때문에 입력단의 노이즈가 출력에 그대로 반영될 수 있다.
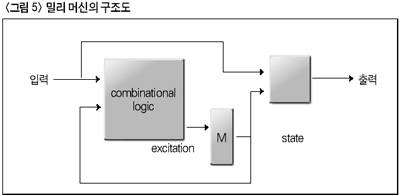
무어 머신
스테이트 머신의 또 하나의 구현 방법으로 무어 머신(moore machine)이 있다. 이는 <그림 6>에서 보는 바와 같이 출력 함수가 현재의 상태만을 입력으로 한다. 따라서 한 개의 상태에 대해서 한 개의 출력만을 갖는다. 이는 밀리 머신에 비해 상태수가 상대적으로 증가하는 단점이 있기는 하지만 입력의 노이즈가 출력에 전달되지 않고 입력 신호의 영향을 다음 단에 전달하지 않기 때문에 밀리 머신보다 좀더 안정적인 동작을 한다고 말할 수 있다.
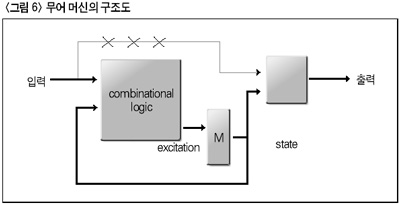
첫 프로젝트, 자판기 구현
이제까지 우리는 하드웨어 기술언어인 VHDL의 기본 골격과 문법적 특징, 모델링 방법 등에 대해 알아봤다. 지금부터는 이러한 VHDL을 이용해 우리의 최종 목표인 자판기의 동작을 묘사할 수 있는 하드웨어 모듈을 구현해 보도록 하자. 일반 소프트웨어 프로그래밍에서도 마찬가지겠지만 특정 제품의 개발을 위해서는 통합 개발 환경(IDE, Integrate Development Environment)이 필요하다. 통합 개발 환경이란 쉽게 말해 프로그래밍하고 컴파일링하며, 끝으로 디버깅에서 실행 파일을 생성하기까지 이를 하나의 환경 아래에서 가능케 해주는 종합 개발 툴이다. 하드웨어의 개발에서도 마찬가지이다. 우리가 이 예제에서 사용할 통합 개발 환경은 Xilinx Foundation이다.
이러한 Xilinx Foundation은 상용 제품이라 자세히 설명하기는 무리가 있지만 이는 하드웨어 개발을 위한 Design Entry Tool과 이러한 디자인된 모듈을 시뮬레이션을 통해 검증해 주는 Design Verification Tool, 그리고 이를 실제 하드웨어적으로 배선/배치에까지의 구현을 책임지는 Design Implementation Tool이 하나로 통합돼 있다. 즉 지난 연재에서 설명한 바 있는 일반 FPGA 관련 설계 절차의 전 과정을 지원하며 또한 VHDL을 이용한 코딩, 시뮬레이션, 합성 등의 모든 과정을 지원한다. <화면 1>은 Xilinx Foundation의 초기 화면이다.

이러한 Xilinx Foundation을 이용해 우리가 작성할 예제는 자판기를 제어하는 모듈이다. 일반 자판기의 원리를 생각해 보기 바란다. 즉 음료를 선택한 후 금액을 넣으면(가령 500원, 100원, 50원, 10원) 해당 음료의 금액과 비교하여 해당 금액 이상의 돈이 들어 올 경우 음료를 출력해 주며 거스름돈을 알맞게 거슬러 준다. 이를 바탕으로 먼저 수행해야 할 작업은 HDL 에디터를 이용해 코딩을 수행하는 작업이다. <화면 2>에서 보는 바와 같이 HDL 편집기를 이용해 프로그래밍한다. 이러한 VHDL의 실제코드는 '이달의 디스켓'의 자판기 내부 동작 관련 코드를 참고하기 바란다.
이렇게 코딩 작업을 마친 후에는 전술한 바와 같이 합성 작업을 거친다. 물론 합성 작업을 하기 전에 일반 소프트웨어 프로그래밍의 문법 검사와 같은 작업을 수행한다. 문법적으로 이상이 없어야 합성 작업을 수행할 수 있다. 이렇게 합성 작업을 수행함에 있어 다시 에러가 검출될 수 있다. 마치 프로그래밍 언어에서 'Syntax Error'는 없지만 'Semantic Error'가 존재하는 것과 같은 이치이다. 이렇게 합성 과정을 거친 이후에는 <화면 3>과 같이 본격적인 회로의 기능적 측면(functional level)에 대한 타이밍 시뮬레이션을 수행한다.
이 시뮬레이션 과정을 거친 후에는 <화면 4>에서 보는 바와 같이 구현 과정을 거친다. 이는 코딩과 시뮬레이션 상에서의 설계가 아닌 실제 특정 하드웨어 칩 모듈에서의 구현을 수행하는 과정이다. 이렇게 구현 과정을 거친 다음에는 끝으로 검증 과정을 거친다. 여기서 다시 한 번 타이밍 시뮬레이션을 수행하는데 이는 앞서 수행한 기술 독립적 타이밍 시뮬레이션과는 차이가 있는 것으로서 특정 업체에서 제공하는 특정 하드웨어 칩을 사용했을 경우 반영해야 할 타이밍의 딜레이를 고려한 시뮬레이션이다. 이런 식으로 최종적인 회로의 검증 과정을 거치면서 실제 특정 FPGA 칩으로의 다운로딩 작업을 거친다.
지금까지 우리는 하드웨어 기술언어인 VHDL을 이용해 칩을 설계하는 절차를 앞서 설명한 두 연재의 배경 지식을 바탕으로 설명했다. 본 연재의 초점은 VHDL이였으므로 자세한 합성 과정과 구현 및 검증 과정에 대한 설명은 많이 축소시킨 것이 사실이다. 하지만 VHDL의 사용 방법만이라도 본 연재를 통해 충분히 숙지한 독자가 나왔다면 필자는 나름대로 만족한다. 끝으로 한 가지만 더 소개하기로 한다. 자판기의 내부 동작에 대한 묘사와는 별개로 또한 일반 사용자가 보기에 자판기의 외부 출력에 대해서 프로그래밍해 볼 수 있을 것이다. 실제로 동전이 입력되어 오는 금액에 따라서 해당 상태로 이동하는 모습과 외부에 동전의 입력이 표시되는 코드를 프로그래밍할 수 있다('이달의 디스켓'참고). 보다 완벽한 코드를 위해 내부 동작과 외부 출력에 대한 코드를 통합해야 할 것이다. 이는 독자 여러분에게 앞으로의 과제로 남긴다.
비메모리 분야의 강국을 꿈꾸며
이번 호에서는 앞서 진행한 두 번의 연재 내용을 토대로 실제 VHDL에 대해 예제를 통해 실습했다. 카운터를 비롯해 특히 CPU의 핵심 모듈이라고 할 수 있는 ALU와 레지스터의 모델링을 VHDL로 직접 해 보았다. 또 우리의 최종 목표인 자판기를 제어하는 모듈도 설계했다 충실히 내용을 숙지한 독자라면 VHDL을 가지고 기본적인 하드웨어 프로그래밍을 수행하는 데 큰 무리가 없으리라고 본다.
사실 디지털 시스템 설계라는 방대한 주제를 가지고 한정된 지면상에서 3회 정도의 분량으로 완전한 이해를 한다는 것은 힘든 일이다. 하지만 이 글을 통해 디지털 시스템을 설계하는 다양한 방법에 대한 소개가 되었으며 특히 그러한 다양한 설계 방법 중에서 하드웨어 기술언어를 이용한 설계 방식에 대해 VHDL이라는 언어를 예로 들어 설명했다. 그리고 이것을 실제 예제를 통해 실습해 보았다. 모쪼록 많은 도움이 되었기를 바란다.
소프트웨어 분야의 기술이 중요시되고 있는 상황에서 IT 강국을 위해서 노력하는 것도 중요한 일일 것이다. 하지만 메모리 분야 세계 1위를 지키고 있는 우리나라의 입장에서 보면 DRAM을 제외한 비메모리 분야에서는 아직 고전을 극복하지 못하고 있는 상태이다. 비메모리 분야 역시 세계적인 강국을 꿈꾸며 보다 많은 하드웨어 엔지니어들이 탄생하기를 기대하며 연재를 마감한다. mas o
정리 : 위윤희 iwish@sbmedia.co.kr
 이달의 디스켓: VHDL_example.zip (5,900 bytes) 이달의 디스켓: VHDL_example.zip (5,900 bytes) 
참고자료
- 'HDL Chip Design' A Practical Guide for Designing, Synthesizing and Simulating ASICs and FPGAs using VHDL or Verilog, Douglas J. Smith, Doone Publications
- Xilinx Foundation을 이용한 디지털 시스템 설계, 이준성 외, 복두 출판사
- VHDL을 이용한 CPLD/FPGA 설계, 차영배 편저, 다다미디어
- 디지털 회로 기술 언어 입문, 논리설계와 HDL의 기초, 정희성 외, 홍릉 과학 출판사
- 주문형 반도체 설계 ASIC DESIGN, 최명렬, 하이테크정보
|
박스기사
래치와 플립플롭의 비교
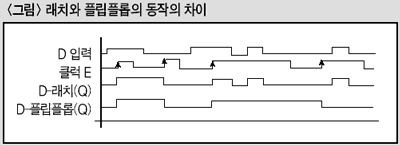
순차 회로를 접할 때마다 항상 등장하는 것이 바로 래치와 플립플롭이다. 래치와 플립플롭이란 두 개의 안정 상태를 갖는 일종의 기억회로를 뜻한다. 이 때 말하는 안정 상태란 회로의 외부로부터 입력을 가하지 않는 한 본래의 값을 유지할 수 있는 회로의 상태를 의미하며 흔히 두 가지의 안정 상태를 말할 경우 이전 값으로 1 혹은 0의 값을 기억하고 있을 수 있다는 의미이다. 그럼 이 둘 사이에 차이점은 무엇일까. 우선 래치의 경우는 레벨 트리거(level trigger)에 의해 동작한다. 따라서 래치는 클럭이 1(high)인 동안 입력의 변화를 그대로 출력에 반영한다. 이에 반해 플립플롭은 에지 트리거(edge trigger)에 의해 동작한다. 따라서 플립플롭은 클럭 펄스가 나타나기 바로 이전의 입력이 출력에 반영되어 다음 클럭 펄스가 나타날 때까지 그 상태를 유지함을 의미한다.
<그림>은 D-타입의 플립플롭과 래치를 사용할 경우를 예로 든 것이다. 회로 구성은 같으나 D 플립플롭은 클럭 펄스가 상승 또는 하강하는 에지 바로 직전의 입력 신호가 출력에 반영되어 다음 클럭 펄스가 나타날 때가지 그 상태를 유지한다. 따라서 인위적인 예제이지만 <그림>에서 보는 바와 같이 클럭 펄스의 폭이 넓어도 D 플립플롭은 출력의 변화가 없지만 래치는 클럭 펄스의 폭이 넓으면 그 동안에 입력의 변화가 출력에 나타나게 된다. 이는 래치보다는 플립플롭이 좀더 안정적인 동작을 보장한다는 의미이기도 하다.
|
|
![]()