Analog
modeling with VHDL and VHDL-AMS essentials
Analog
modeling with VHDL and VHDL-AMS essentials
prepared by P. Bakowski

 Introduction
Introduction
The modeling of analog systems with VHDL is possible
but limited by the inherent discrete-event simulation mode.
The application of discrete-event modeling mode
to analog systems requires two consecutive transformations:
-
the mapping of analog continuous-time systems
into analog discrete-time systems based on data-sampling techniques
-
the mapping of analog discrete-time systems into
VHDL syntax and semantics.
This solution works well for relatively simple models. Main aspects of
this kind of modeling and few examples of VHDL code used to model analog
circuits are given in the first part of our presentation.
Complex analog models possibly composed from several entities require
more powerful modeling environment provided by VHDL-AMS (IEEE 1076.1).
This analog extension to VHDL called VHDL-AMS is discussed briefly
in the second part of this presentation. Much more complete presentation
of VHDL-AMS is elaborated by Ken Bakalar, Ernst Christen
and Alain Vachoux in the form of VHDL-AMS
Tutorial.
Content: analog
models in VHDL, VHDL-AMS: quantities,
simultaneous statements, structural
descriptions, procedural statements, simulation
time and cycle, digital-to-analog and analog-to-digital
events, break statement, bouncing
ball
Other sites:
This short tutorial describes the basic techniques used for analog circuit
simulation in both the temporal and the frequential domains.
 VHDL
and analog systems
VHDL
and analog systems
VHDL simulation model is based on a discrete-event
simulation cycle. Modeling of analog systems with discrete-event simulation
mode requires the translation of continuous-time systems into data-sampled
systems. This translation is an approximation of the continuous waveforms
by a finite set of samples. If the analog waveform is frequency bandwidth
limited, then the sampling inaccuracy can be eliminated provided the Nyquist
Criterion is satisfied. The narrower is the bandwidth the smaller is
the number of samples.
The simplest to model an analog system behavior is to provide at its
input sinusoidal stimuli. In case of VHDL model we can use a sampled
sinusoidal stimuli. For simple linear time-invariant systems the response
is a sinusoid. The amplitude and the phase of the response characterizes
the system.
More precisely, the stimulated system goes through two phases;
-
the initial phase is a transient situation normally described by a set
of differential and algebraic equations and
-
the steady-state response to which the excitated system converges after
a certain time delay.
The following VHDL example describes a simple operational amplifier. In
this description we model only the steady-state response of the amplifier.
The description of the amplifier is preceded by the definition of analog
data package. The analog_defs package contains some basic
definitions of physical types used in the following models. Note that the
type analog_signal is a record of voltage and current types.
-
package analog is
-
type voltage is
range 0 to integer'high
-
units
-
mV;
-- milivolts
-
V = 1000 mv; -- volts
-
end units;
-
type current is
range 0 to integer'high
-
units
-
mA;
-- miliamperes
-
A = 1000 mA; -- amperes
-
end units;
-
type impedance is
range 0 to 1E9
-
units
-
Ohm;
-- ohms
-
KOhm = 1000 Ohm; -- kiloohms
-
MOhm = 1000 KOhm; -- megaohms
-
end units;
-
type analog_signal is
record
-
v: voltage;
-
i: current;
-
end record;
-
end analog;
-
-- operational amplifier
-
use work.analog.all;
-
entity operational_amp is
-
generic(opamp_delay: time:=15 ns);
-
port(plus_in, minus_in: in
analog_signal;
-
output: out analog_signal;
-
pwr,gnd: in analog_signal);
-
end op_amp;
-
-- operational amplifier architecture
-
architecture behavioral of
operational_amp is
-
constant voltage_gain: real:= 500.0;
-
begin
-
output.v <= voltage_gain * (plus_in.v - minus_in.v) after
opamp_delay;
-
end behavioral;
 VHDL-AMS
VHDL-AMS
VHDL-AMS (1076.1) is a superset of VHDL'93 which allows to describe
mixed-signal and analogue systems that exhibit continuous behavior. The
design of analogue extension to VHDL began in 1993. This work it
was supported by DACS (Design Automation Standards Committee of the Computer
Society of the IEEE) and by JESSI (Joint European Silicon Software Initiative)
and several industrial organizations.
The essential enhancements introduced into VHDL-AMS are:
-
support for quantities and terminals representing analogue signals and
network connectivity
-
support for simultaneous equations to model analogue behavior
-
support for break mechanism required to model discontinuities in analogue
signals
The modeling space covered by VHDL-AMS is presented in the table below:
|
continuous time |
discrete time |
| continuous signal |
differential and algebraic equation (DEA) systems
analog components and circuits
|
switched capacitor circuits
sample and hold
|
| discrete signal |
digital-to-analog converters
|
analog-to-digital converters
sampled systems
digital components and systems
|
Quantities
Quantity is a new class of objets allowing to model analytic functions
in time and frequency domains. Quantities may represent voltage, current,
velocity and other physical values evolving continuously in time
and/or in frequency domains. Quantities are simple or complex objects built
from floating point types.
Quantities may be declared inside an architecture as internal object
or in a port list as imported/exported object.
-
quantity ra,rb: real;
-
entity simple is
-
port(quantity qin: in
real; quantity qout: out real); -- interface
quantity
-
end simple;
The quantities allows to describe the systems of ordinary differential
and algebraic equations (DAEs) having the form of:
-
F(dX/dt,X,t) = 0
where F is a vector of expressions, X is the vector of unknowns
in the equations, dX/dt is the vector of derivatives of the unknowns
with respect to time and t is time. Most of DAEs have no analytic
solution, in practice they must be resolved by use of numerical methods.
VHDL-AMS provides a notation for DAEs but does not provide any specific
techniques for their solution. This approach allows the implementer to
choose the appropriate method (analog solver) for the solution of the equations.
The precision of the solution is indicated through the concept of tolerance.
The tolerance may be selected according to the number of accurate digits
needed in the solution.
VHDL-AMS supports the notion of tolerance groups defined as a collection
of solution elements and characteristics having the same accuracy requirements.
The type of tolerance (tolerance code) is a string that can be defined
by the user e.g.. "maxtol", "abstol", .. .
-
quantity cur1: current tolerance
"abstol";
There are two kinds of implicit quantities associated to an explicit quantity
quant:
-
derivated quantity with respect to time denoted as quant'dot
and
-
integer quantity over time (from time 0.0 to now)
quant'integ.
Branch quantity
Branch quantities are used to express the values of electrical natures
between two terminals. There are two kind of branch quantities:
-
across quantities like voltage
and
-
through quantities like current.
More generally, the branch quantities reflect different natures of physical
phenomena (see some examples below)
| nature |
across |
through |
| electrical |
voltage |
current |
| mechanical |
velocity |
force |
| thermal |
temperature |
heat float rate |
The constitutive equations of conservative systems are described by relating
the across and through quantities of one or several branches.
-
subtype voltage
is real tolerance
"maxtol_volt";
-
subtype current
is real tolerance
"maxtol_curr";
-
nature electrical
is voltage across current through;
-- declaration of a nature
-
terminal tel1,tel2: electrical;
-
quantity vol across
i1,i2 through tel1 to
tel2;
-
The attributes across and
through allow the user to
extract the corresponding natures of the indicated object:
-
-
tel1'across is voltage
-
tel1'through is current
-
The nature or nature type may be declared as a vector:
-
nature electrical_vector
is array (integer
range <>)
of electrical;
-
subnature vel8
is electrical_vector(7
downto 0);
-
quantity elvec1,elvec2:
vel8;
-
Terminal, like a signal can be a port of an entity.
The following example shows a simple resistor model with two terminals,
the input terminal rin and the output terminal rout:
-
entity resistor
is
-
port(terminal
rin,rout: electrical);
-
end resistor;
-
If a branch quantity is declared as "simple terminal"
then a reference terminal (node) is created. It is designated by ter'reference
attribute. The reference
attribute is considered as ground terminal,. A simple terminal declaration
creates a branch to ground.
-
The declaration of a terminal itself provides
two quantities:
the reference quantity (ter'reference)
and
the contribution quantity (ter'contribution)
which is a through quantity whose value is equal to the sum of all
through quantities incident to ter and taken with appropriate
sign.
Simultaneous statements
The description of continuous behavior needs a new
kind of notation not available in VHDL 1076. This notation is introduced
in VHDL-AMS as simultaneous statements. Simultaneous statement can
appear anywhere a concurrent signal assignment is allowed. The syntax of
a simultaneous statement is as follows:
-
simple_expression == simple_expression
The expression may refer to quantities, signals,
constants, shared variables, literals and functions.
For example, the constitutive equation of a resistor
is written as :
-
i == v/r;
where v is a cross quantity representing the voltage
and i is a current flowing through the resistor
-
entity resistor
is
-
generic(r:real:=1.0E2);
-
port(terminal
rin,rout: electrical);
-
end resistor;
-
architecture
simple of resistor
is
-
begin
-
quantity v across
i through rin
to rout;
-
begin
-
i == v/r; -- simultaneous statement
-
end simple;
-
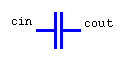
-
entity
capacitor is
-
generic(c:real:=1.0E-8);
-
port(terminal
cin,cout: electrical);
-
end capacitor;
-
--
-
architecture
simple of capacitor
is
-
begin
-
quantity v across
i through cin
to cout;
-
begin
-
i == c*v'dot;
-- simultaneous statement
-
end simple;
Simultaneous statements are the equations representing the conservative
laws. These laws are denoted by characteristic expressions.
The analog solver determines the value of each quantity such that the
values of all characteristic expressions are close to zero and thus solves
the DAEs of the model. Each characteristic expression belongs to a tolerance
group. The default tolerance group, is the tolerance group of the left
hand side quantity.
For example the following model of a resistor (r) and and impedance
(l) (inductor) an its a simultaneous statement corresponding to its
characteristic expression ( v - r*i - l*i'dot):
-
v == r*i + l*i'dot;
-
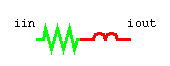
-
entity inductor
is
-
generic(ir:real:=1.0E2;
il:real=1.0E-2);
-
port(terminal
iin,iout: electrical);
-
end inductor;
-
architecture
simple of inductor
is
-
quantity vi across
ii through iin
to iout;
-
begin
-
vi == ir*i + il'dot*il
tolerance "maxtol";
-
-- simultaneous statement; tolerance "maxtol"
of vi
-
end simple;
More complex models may integrate multiple simultaneous
statements which in turn may be selected according to the external or/and
internal conditions. An example of such model may be a limiting voltage
amplifier:
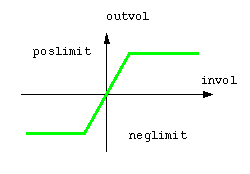
-
architecture simult
of amp_lim is
-
quantity invol
across involp
to involn;
-
quantity outvol
across outvolp
to outvoln;
-
begin
-
if
(invol*gain > poslimit) use
-
volout == poslimit;
-- simultaneous statement
-
elsif
(invol*gain < neglimit) use
-
outvol == neglimit;
-- simultaneous statement
-
else
-
outvol == invol*gain; --
simultaneous statement
-
end use;
-
end simult;
Example of diode component model . Note that diode is a non linear
component. Its description requires the use of conditional statements allowing
to select the characteristic equations relative to different operational
intervals.
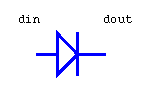
-
entity diode
is
-
port(terminal
din,dout: electrical);
-
end diode;
-
--
-
architecture
simple of diode
is
-
quantity dv across
di through din
to dout;
-
constant VT:
real := 0.026;
-
constant ISS:
real := 1.0E-12; -- saturation current
-
begin
-
di == ISS*(exp(dv/VT)-1.0);
-- normal operational interval
-
end simple;
-
--
-
architecture
complete of diode
is
-
quantity dv across
di through din
to dout;
-
constant VT:
real := 0.026;
-
constant BV:
real := 100.0;
-
constant IBV:
real := 0.001;
-
constant ISS:
real := 1.0E-12; -- saturation current
-
constant NISS:
real := -1.0E-12; -- negative saturation current
-
begin
-
if
(dv >=(-5.0*VT)) use
-
di == ISS*(exp(dv/VT)-1.0);
-
elsif
((dv >=(-5.0*VT)) and
(dv > -BV)) use
-
di == ISS;
-
elsif
(dv = BV) use
-
di == - IBV;
-
else
-
di == NISS*(exp(-(BV+dv)/VT)-1.0+BV/VT);
-
end use;
-
end complete;
Building structures
The possibility to create behavioral analog descriptions
for complex analog components is one of the main advantages of VHDL-AMS.
However, with VHDL-AMS one can also build structural descriptions from
the interconnected simple components. Note that this style of modeling
is specific to Spice design environments.
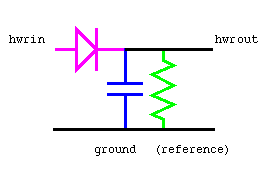
For example a half wave rectifier built from a diode,
capacitor and resistor components can be described as follows ( resistor
model , diode model and capacitor
model are presented above):
-
--
-
entity hwr is
-
generic(r: real:=
100.0; c:real:=1.0E-8);
-
port(terminal
hwrin,hwrout: electrical);
-
end hwr;
-
--
-
architecture
structural of
hwr is
-
-- component declaration
-
component
comp_resistor
-
generic(r:real);
-
port(terminal
rin,rout: electrical);
-
end component;
-
--
-
component comp_diode
is
-
port(terminal
din,dout: electrical);
-
end component;
-
--
-
component comp_capacitor
is
-
generic(c:real);
-
port(terminal
cin,cout: electrical);
-
end component;
-
-- component configuration
-
for res_unit1:
comp_resistor use
work.resistor(simple);
-
for cap_unit1:
comp_capacitor use
work.capacitor(simple);
-
for diode_unit1:
comp_diode use
work.diode(simple);
-
--
-
begin
-
-- component instantiation
-
diode_unit1: port
map(hwrin,hwrout);
-
-- electrical'reference
is implicit ground terminal
-
cap_unit1: port
map(hwrout,electrical'reference);
-
res_unit1: port
map(hwrout,electrical'reference);
-
end structural;
Procedural statements
Procedural statements allows to describe the DAEs
using sequential operations. A procedural statement can include any sequential
statement of the VHDL language except wait statements and signal assignments.
The following is an example of the voltage amplifier architecture expressed
with procedural statements.
-
architecture proced
of amp_lim is
-
quantity invol
across involp
to involn;
-
quantity outvol
across outvolp
to outvoln;
-
begin
-
procedural
-
variable
volt: voltage;
-
begin
-
volt := invol*gain;
-- procedural statement
-
outvol := volt;
-
if
(volt > poslimit) then
-
outvol := poslimit;
-- procedural statement
-
elsif
(volt < neglimit) then
-
outvol:= neglimit;
-- procedural statement
-
end if;
-
end procedural;
-
end proced;
--
Simulation time
and cycle
The simulation time for mixed analog-digital simulation
is represented by universal_time. The precision of universal_time is sufficiently
high to represent the physical time required by the analog solver. The
function now is overloaded to correspond to the nearest value of
current universal (physical) time.
The analog simulation cycle covers the time
required for the execution of analog solver . The analog solver executes
in each simulation cycle just before the current simulation time advances;
the solver establishes a sequence of solutions to the DAES at suitable
intervals between the last event and the time of the next event. The value
of resolved quantity is always correct when a digital process reads the
quantity.
Analog-digital and digital-analog events
The analog solver terminates the operation at any analog-to-digital event
generated by designated thresholds. The thresholds may be detected by predefined
attribute above. For any scalar
quantity q greater then level the attribute
q'above(level) generates
a boolean signal with true value, otherwise the signal
value is false.
-
entity atodconv
is -- simple
analog-to-digital converter
-
generic(level:
real:= 4.5);
-
port(terminal
adin,ref: electrical; signal
adout: out bit);
-
end atodconv;
-
architecture
simple of atodconv
is
-
quantity vad
across adin to
ref;
-
begin
-
adout <= '1' when
vad'above(level)
else '0';
end simple;
A digital process that is sensitive to the signal generated by q'above(level)
expression executes at the exact time of the threshold crossing. Such a
time is called offset time. Any process resuming as a consequence of a
delta-delayed signal assignment in a process executing at an offset aligns
the delta time to the same offset time.
break
statement
The digital to analog conversion needs a special mechanism allowing to
re-initialize the analog process evaluation when a specific condition occurs.
This condition is called break condition and it is detected by a new mechanism
and keyword break. The execution of break statement creates an event on
implicit break signal. The analog solver assumes the analog discontinuity
whenever the driver of break signal is active. the break statement allows
for specifying new initial conditions for selected quantities to be applied
after the detected discontinuity.
The following example shows the use of break statement for the description
of a simple DA converter:
-
entity dtoaconv
is -- simple
digital-to-analog converter
-
generic(vref:
real:=0.01);
-
port(terminal
daout,ref: electrical; signal
dain: in bit_vector(7
downto 0));
-
end dtoaconv;
-
architecture
simple of dtoaconv
is
-
quantity vda
across daout
to ref;
-
begin
-
procedural
-
variable bvalue:
real=0.0;
-
for i
in dain'right
to dain'left
loop
-
if dain(i)='1'
then
-
bvalue := real(2**i) + bvalue;
-
end if;
-
end loop;
-
end procedural;
-
break on dain;
-- the architecture re-evaluated if break
on dain
-
daout == vref*bvalue ;
-
end simple;
The break statement allows to detect the events in
order to reinitialize the evaluation of analog processes. The case of digital
to analog converter is a specific one. In general, the break statement
is used to impose some initial conditions on analog resolution process
when the process itself faces discontinuity.
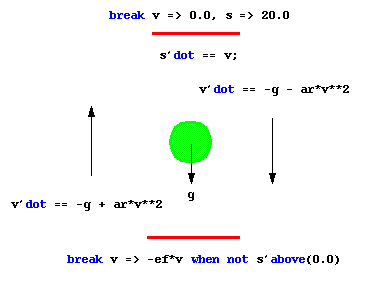
Bouncing ball
A well known example of a process with discontinuity
is bouncing ball model. In this example there are two break conditions
(discontinuity conditions); the first break is the initial condition; the
second break condition describes the behavior of the ball when it hits
the ground.
-
architecture simple
of bouncing_ball is
-
quantity s:real; -- amplitude
-
quantity v:real; -- velocity
-
constant g:real:= 9.81; -- gravity
constant (terrestrial gravity acceleration)
-
constant ar:real:= 0.01; -- air resistance
factor
-
constant ef:real:= 0.9; -- elasticity
factor
-
begin
-
velocity: v == s'dot;
-
if v < 0.0 use
-
v'dot == -g + ar*v**2;
-
else
-
v'dot == -g - ar*v**2;
-
end use;
-
breakcond1: break
v => 0.0, s => 20; -- initial conditions
-
breakcond2: break
v => - ef*v when not s'above(0.0);
-- ball hits ground
-
end simple;
Note that if the elasticity factor (ef)
equals 1 and the air resistance factor (ar) equals
0, the ball bounces infinitely.
 Analog
modeling with VHDL and VHDL-AMS essentials
Analog
modeling with VHDL and VHDL-AMS essentials